Numerical Modeling of Adhesion in Interactive Simulations
Multi-modal virtual surgical trainers and planners that are equipped with interactive physics-based simulations are becoming common in curricula for medical training. They help to hone procedural and broader skills, thereby improving overall surgical outcomes. These simulators demand high frame rates and high-fidelity simulations [1]. To improve medical training, a team aimed to increase the fidelity of surgical simulations [1].
In medical training, adhesive contact may be observed between surgical tools and internal organs [1]. This contact is caused by adhesive forces [2]. Adhesive forces tend to oppose the relative motion of bodies under contact and result from material damage that occurs on a microscopic scale [3].
To observe the evolution of adhesive forces over time, the team modeled an elastic block as it fell under gravity from a preset height onto a rigid plane. Figure 1 plots the evolution of adhesive forces over time for different levels of adhesion stiffness. As the figure indicates, the forces fluctuated in response to the cycling of the internal energy of the block between potential (elastic) energy and kinetic energy. For lower adhesion stiffness, the elastic block did not detach from the plane upon initial contact. For higher adhesion stiffness, the adhesive forces did not prevent the block from detaching from the plane upon first impact.
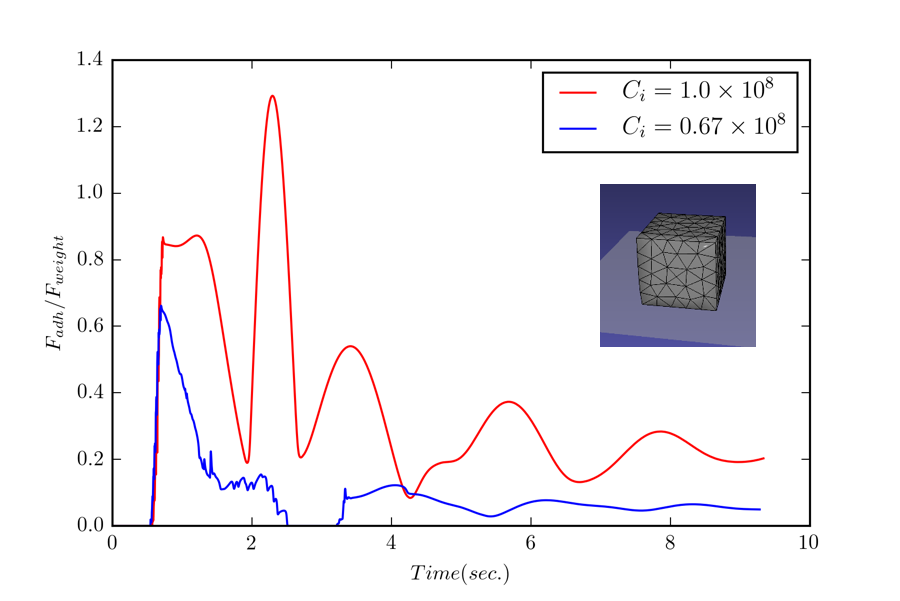
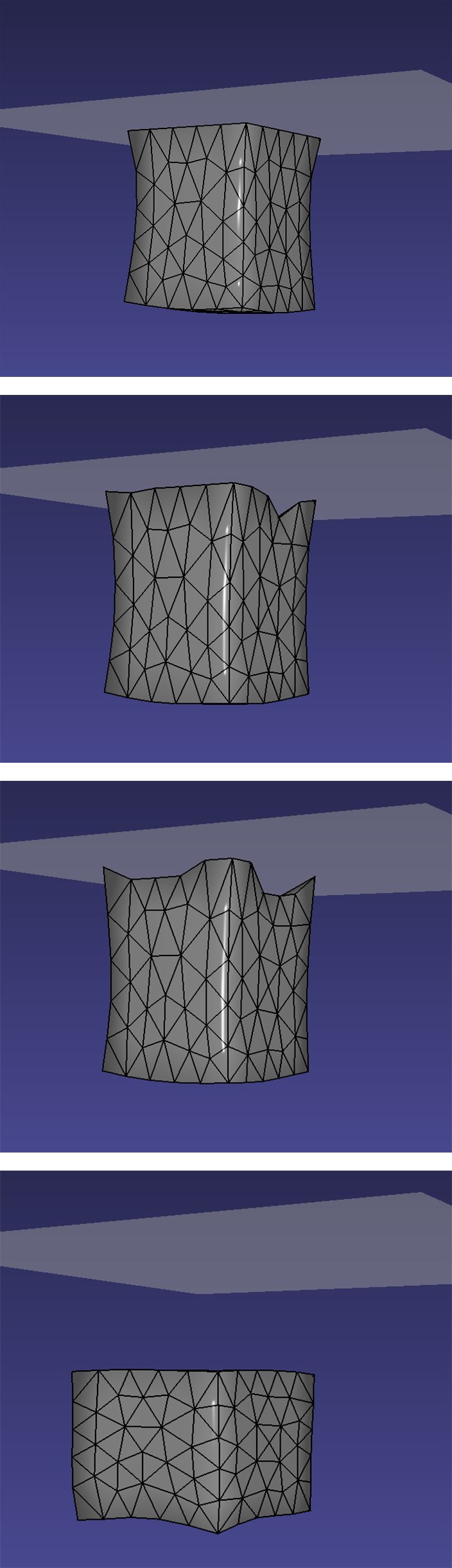
Figure 2 shows various stages of detachment for the same block under the influence of its own weight over time. Modeling such simulations with adhesion in real time involves formulating non-contiguous, regime-based, physical phenomena, which generally produces the mixed linear complementarity problem (MLCP) [4]. Numerical methods that formulate these phenomena combine traditional ideas for solving linear algebraic systems (e.g., fixed-point iteration and pivoting [5]) with a decision-making step. This step implements a metaphorical “if-else” to find the solution to the MLCP [6].
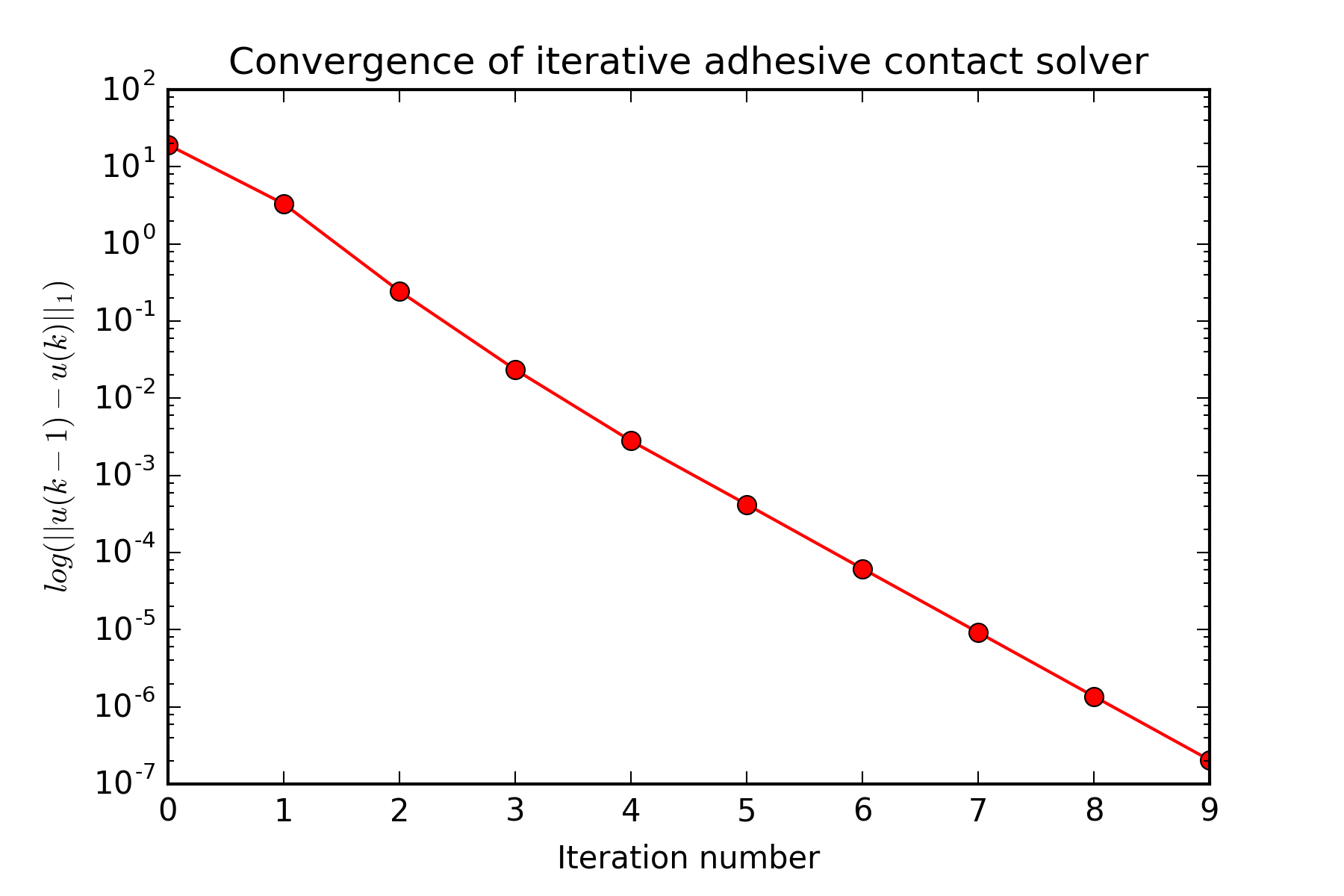
The team built on a modified version of a previously known solver for the MLCP: iterative constraint anticipation (ICA) [6]. ICA can be employed in real time. The modified version on which the team built is described in Arikatla et al. [7]. For its work, the team proposed a new algorithm: iterative adhesive contact solver (IACS) [1]. Figure 3 outlines IACS.

![]() computational complexity. Thus, the approach has limitations when applied to real-time simulations [1].
computational complexity. Thus, the approach has limitations when applied to real-time simulations [1].
Alternatively, to refrain from inverting the system matrix, IACS splits the unknowns into contact states (bonding or debonding), contact forces (adhesive and normal) and displacements [1]. This allows the adhesive forces to be treated explicitly. In addition, whereas the approach in Arikatla et al. [7] first estimates the states/forces in an approximate solver and then solves for the final state, IACS continually updates the states and forces until it undergoes convergence [1]. According to the convergence criteria, IACS stops when the change in the displacement field between consecutive iterations is less than a preset threshold.
It is important to note that the converged solution that is based on this criteria is not guaranteed to be the solution to the MLCP. The fact that the unknown contact states and adhesive forces are not implicitly formulated as part of the MLCP system makes it difficult to establish practical residual-based convergence criteria.
Testing and Future Work
As Figure 4 depicts, the team tested IACS on a case in which a rigid tool interacted with a liver [1]. The testing focused on adhesive forces; it did not consider frictional forces, which are generally coupled with adhesive forces.

Source: Arikatla et al. [1].
References
- Arikatla, Venkata S., Mohit Tyagi, Xinyu G. Chen, Suvranu De and Andinet Enquobahrie. “An iterative approach for modeling adhesion in surgical simulations.” CMBE 2017 Proceedings 2 (2017): 810-813.
- Kenneth R. Shull. “Contact mechanics and the adhesion of soft solids.” Materials Science and Engineering: R: Reports 36 (2002): 1-45.
- Sacco, Elio, and Frédéric Lebon. “A damage–friction interface model derived from micromechanical approach.” International Journal of Solids and Structures 49 (2012): 3666-3680.
- Cottle, Richard W., Jong-Shi Pang and Richard E. Stone. The Linear Complementarity Problem. Society for Industrial and Applied Mathematics, 2009.
- Saad, Yousef. Iterative methods for Sparse Linear Systems Second Edition. Society for Industrial and Applied Mathematics, 2003.
- Otaduy, Miguel A., Rasmus Tamstorf, Dennis Steinemann and Markus Gross. “Implicit Contact Handling for Deformable Objects.” Computer Graphics Forum 28 (2009): 559-568.
- Arikatla, Venkata S., and Suvranu De. “An iterative predictor–corrector approach for modeling static and kinetic friction in interactive simulations.” Graphical Models, 82 (2015): 29-42.
- Raous, Michel, Laurent Cangémi and Marius Cocu. “A consistent model coupling adhesion, friction, and unilateral contact.” Computer Methods in Applied Mechanics and Engineering 177 (1999): 389-399.
- Gascón, Jorge, Javier S. Zurdo and Miguel A. Otaduy. “Constraint-Based Simulation of Adhesive Contact.” Proceedings of the 2010 ACM SIGGRAPH/Eurographics Symposium on Computer Animation (2010): 39-44.
Acknowledgement
This material is based upon work supported by the United States Army Medical Research Acquisition Activity (USAMRAA) under Contract No. W81XWH-16-C-0094. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the USAMRAA.
Research reported in this publication was supported by the Office Of The Director, National Institutes Of Health of the National Institutes of Health under Award Number R44OD018334. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
 Sreekanth Arikatla is a senior research and development engineer at Kitware. His interests include numerical methods, computational mechanics, computer graphics and virtual reality.
Sreekanth Arikatla is a senior research and development engineer at Kitware. His interests include numerical methods, computational mechanics, computer graphics and virtual reality.
 Mohit Tyagi completed a research and development internship on the medical computing team at Kitware. He currently works at Altair Engineering, India, as a solver development engineer. His interests include inverse problems, computational mechanics and numerical methods.
Mohit Tyagi completed a research and development internship on the medical computing team at Kitware. He currently works at Altair Engineering, India, as a solver development engineer. His interests include inverse problems, computational mechanics and numerical methods.
 Andinet Enquobahrie is the director of medical computing at Kitware, where he manages projects for image-guided intervention, quantitative imaging and surgical simulation.
Andinet Enquobahrie is the director of medical computing at Kitware, where he manages projects for image-guided intervention, quantitative imaging and surgical simulation.
 Grace Chen is a senior project engineer of computational medicine and biology at CFD Research Corporation. Her research focuses on computational biomechanics, injury prevention and mitigation as well as composite damage and failure modeling.
Grace Chen is a senior project engineer of computational medicine and biology at CFD Research Corporation. Her research focuses on computational biomechanics, injury prevention and mitigation as well as composite damage and failure modeling.