MAP-Tk 0.6.0 Release

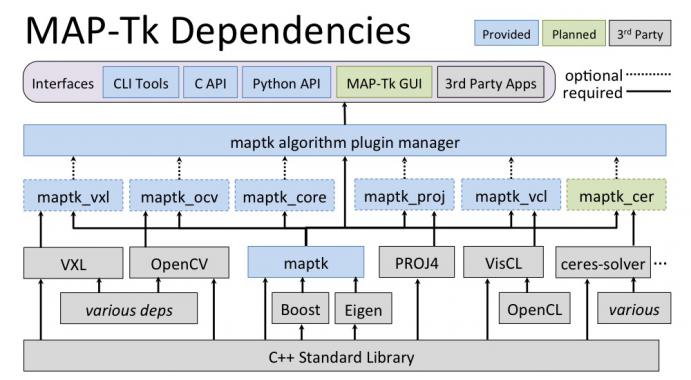
MapTK 0.6.0 is a major release that offers advanced functionality, new algorithms, and a preview of features that will be introduced in the 1.0.0 release, including C and Python bindings. The 0.6 release also features a switch to Eigen, which provides a core linear algebra data structure and additional algorithms (e.g., matrix and vector).
Another highlight of the release is significant restructuring, which replaces the module framework with dynamically loaded plugins. The plugin framework allows new algorithms to be loaded at runtime, but does not require MAP-Tk to be recompiled or tools to be built on top of MAP-TK. In addition, a new core plugin is available for core algorithm implementations that were previously in the MAP-Tk library. While abstract algorithm declarations remain in the main MAP-Tk library, concrete implementations of these algorithms are now loaded through plugins. This means that you can write your own plugin, drop it into the plugins directory, and insert your algorithm implementations into a MAP-Tk pipeline with merely a configuration file change.
The release also features several updates to MAP-Tk’s build system, library, plugins, test system, and tools. For a complete list of updates made to MAP-Tk since version 0.5, please visit https://github.com/Kitware/maptk/releases/tag/v0.6.0.
As we work toward version 1.0.0, we may have a few more intermediate releases. The next release of MAP-Tk will include a faster and more powerful bundle adjustment backend provided by Ceres Solver. We are also further refactoring the MAP-Tk code to allow for better integration across other KWIVER tools. We expect an initial GUI interface based on VIVIA to be ready soon, as well as an online processing variant of the MAP-Tk pipeline powered by sprokit. Stay tuned for upcoming releases of MAP-Tk!
About MAP-Tk
The Motion-Imagery Aerial Photogrammetry Toolkit (MAP-Tk) is an open-source C++ collection of libraries and tools for making measurements from aerial video. Its initial capability focuses on estimating the camera flight trajectory and sparse 3D point cloud of a scene.